[latexpage]
3次関数には意外と知られていない便利なテクニックが存在します
それは「8分割パレット」です!
今回はそんな8分割パレットの使い方や便利な点を解説します
8分割パレットとは
そもそも8分割パレット自体聞き慣れない単語だと思うので解説します
8分割パレットとは下図の赤線のように三次関数に書き込むことができる8分割した長方形のことです
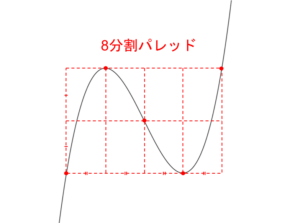
またグラフ上の赤い点は「極小値、極大値、変曲点(グラフの中心)、極大値と同じ値を取る点、極小値と同じ値を取る点」の5つです
この5点と8分割パレット上の位置との対応関係は以下のようになります
| 三次関数 | 8分割パレット |
| 極小値と同じ値を取る点 | 左下 |
| 極大値 | 左上から2番目 |
| 変曲点 | 真ん中 |
| 極小値 | 右下から2番目 |
| 極大値と同じ値を取る点 | 右上 |
この対応関係を意識すると8分割パレットが書きやすいです
頑張って3次関数上に書き込めるようにしましょう!
便利な点
次になぜこの8分割パレットが便利なのか具体例を用いて説明します
以下の関数$f(x)$が問題で与えられ、グラフ化したい場合を考えましょう
$$f(x)=\frac{1}{3}x^3-ax^2-3a^2{x}$$
(ただし$a>0$)
微分すると
\begin{align}
f'(x) &=x^2-2ax-3a^2 \\
&=(x+a)(x-3a)
\end{align}
となるので増減表を用いてグラフを書くと以下のようになります!
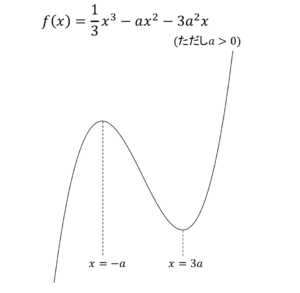
ここまでは通常通りですね
では8分割パレットを書き込んでみましょう
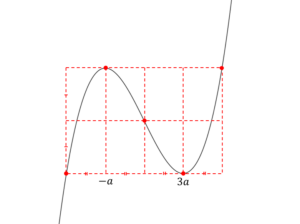
8分割パレットを見ると、真ん中の変曲点は-aと3aの中間地点なので、x=aだとわかりますよね
また8分割パレットの8つの長方形の横の長さが2aだということもわかるので5点すべてのxの値がわかり、以下のように書き込むことができます!
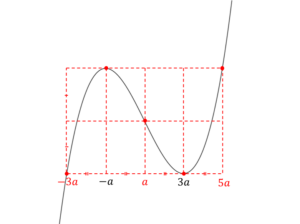
つまり8分割パレットを書き込むことで本来求めることが出来ていなかった「変曲点」「極大値と同じ値を取る点」「極小値と同じ値を取る点」の3点のxの値を瞬時にだすことができるんです!
これらの値が必要になる問題も多く、8分割パレットを用いない場合は地道に計算する必要があるので、瞬時に求めることが出来るのはかなり便利だと思います
また今回の関数ではこれだけでは終わりません
上のグラフをよく見ると、極大値と変曲点のxの値はそれぞれ-aとaで、その真ん中がx=0とわかるので、以下のようにy軸を引くことが出来ます
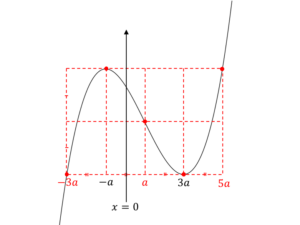
そして今$f(x)=\frac{1}{3}x^3-ax^2-3a^2{x}$よりx=0のとき$f(0)=0$となることから、y軸とグラフの交点がちょうど原点だとわかるのでx軸もひくことが出来ます

最後に8分割パレットを用いる前と後のグラフを比較してみましょう!
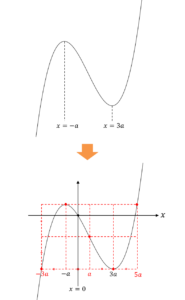
かなり具体的にグラフの概形が把握できました!
まとめ
以上より8分割パレットを利用するメリットは以下の2つです
- 「変曲点」「極大値と同じ値を取る点」「極小値と同じ値を取る点」の3点のxの値を瞬時に出せる
- x軸やy軸が引ける(ことがある)
いろんな問題で応用が効き非常に便利なので、ぜひマスターしてみてください!