区別がある？区別がない？組分け問題をイラストで分かりやすく解説！

組み分け問題は「とりあえず解けるけど理由は分からない」となりがちな分野です
特に区別をなくすやり方を丸暗記して「とりあえず3!で割る」のような解き方をしている人は多いと感じます
今回はそんな組み分け問題をイラストを用いて本質から解説していきます

この解説を読んで貰えれば、その場しのぎの丸暗記を卒業して、どんな難問にも対応出来るようになるよ！

では行きましょう！

今回のポイント

今回抑えて欲しい内容は以下の通りです

1. 振り分け先が区別できるかできないか正しく把握できるようにする
2. 組み分け問題の解き方2ステップをマスターする
3. 組分け問題を丸暗記でなく、納得感を持って解けるようにする

では説明していきます！

組み分け問題とは？

組み分け問題とは、ヒトやモノを複数グループに振り分けていく問題です
例えば以下のような問題です

問題(1)〜(4)は、いずれもA〜Fの6人を数や色が異なる３つのグループ(組)に振り分けていますよね！
これが組み分け問題です
この4パターンを抑えれば組み分け問題はもう怖くありません！
なので今回はこの4つを解けるように解説します！

区別できるできないとは？

組み分け問題では、振り分け先どうしが互いに区別できるかどうかで解き方が変わってきます
まずは先ほどの4パターンの問題を見て、振り分け先の各組が互いに区別できるかどうか考えて見てください

いきなり区別できるか考えろと言われてもいまいち分かりづらいですよね...
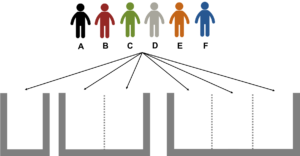
ではもう少し分かりやすくするために、A〜Fの６人と(1)〜(4)の振り分け先をイラストにしてみましょう！

A〜Fの6人をそれぞれ6色で表し、各組は部屋に見立てて表現しました
このイラストを使って振り分け先の区別が互いにつくかどうか考えると、

(1)は各部屋に入る人数が異なるので、3部屋は互いに区別できる
(2)は人数は同じだが、それぞれ色が異なるので、3部屋は互いに区別できる
(3)は各部屋に入る人数と色が同じで全く同じ見た目なので、3部屋は互いに区別できない
(4)は1人しか入れない2部屋どうしは区別できないが、4人が入る1部屋は他と区別できる

となります

要するに、見た目が全く同じ部屋は区別できないけど、各部屋の色やサイズが異なっていたら見た目が異なるので区別できるってことだね！

ではいよいよ組分け問題の解き方を解説していきましょう！

組分け問題の解き方

組分け問題は以下の２つのステップを踏めば必ず解けます！

つまり先程イラストで解説した、振り分け先の区別の有無に関わらず、
まずstep1では全ての部屋が区別できるとして各部屋に人を振り分けていきます！
そして本当は区別がない場合のみ、step2に進み、部屋の区別をなくして真の値を求める、ことになります

これだけだと何が言いたいのかわからないよね...

ではこれがどういう意味か、問題(1)〜(4)の解き方で具体的に見ていきます！

問題(1)の解き方

(1)では各部屋に入る人数が1,2,3人と異なり、各部屋の見た目がどれも異なるので、3部屋全ての区別が出来ます
ではstep1とstep2の順に考えていきましょう

step1

step1では「全ての部屋が区別できるとして各部屋に人を振り分けていく」のでしたね
今回3部屋とも初めから区別がつくので、早速各部屋に人を振り分けていきましょう
具体的には、1部屋ずつ順番に部屋を指定し、その指定した部屋に入る人物をA〜Fの6人から選びます

どの部屋から指定するかは自由ですので、
ここでは、まず定員が1名の部屋を指定し、そこに入る一人を6人から選ぶと、₆C₁= 6 (通り)です
次に、定員が2名の部屋を指定し、そこに入る一人を残りの5人から選ぶと、₅C₂ = 10 (通り)となります
最後は定員が3名の部屋を指定します
そこに入る３人は必然的に残りの3人となり、₃C₃ = 1 (通り)です

よって振り分け方の総数は、これらをかけ合わせて₆C₁×₅C₂×₃C₃= 60 (通り)となります

部屋を指定する順番は何でも良いけど、人数が少ない部屋から選んだ方が計算が楽になるよ♪

step2

step2には本当は各部屋に区別がなかった場合のみ進むのでした
今回は初めから3部屋とも区別がついたので特にstep2を考えず、60通りがそのまま答えとなります

問題(2)の解き方

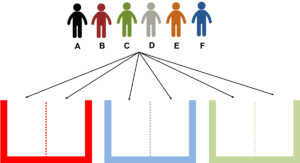
(2)では各部屋に入る人数は同じだが、それぞれ色が異なり見た目に違いがあるため、3部屋とも区別出来ます

step1

(1)と同様3部屋とも区別が出来るので、好きな色の部屋から順番にA〜Fの6人を入れていきます

「赤→青→緑」や「青→赤→緑」といった風に好きな順番で大丈夫だよ♪

いずれの選び方をしても分け方の総数は₆C₂×₄C₂ = 90 (通り)となります

step2

(1)と同じく、初めから区別がついていたのでstep2には移らず90通りがそのまま答えです

問題(3)の解き方

ここからが問題(1)(2)と異なってきます！
問題(3)では各部屋に入る人数と色が全く同じなので、3部屋とも見た目が全く同じで区別が出来ません

　step1

step1では、区別が出来ない場合も、まずは区別が出来るとして考えていくので、
各部屋に赤・青・緑色をつけて区別出来るようにしてあげましょう

そして(2)と同様に好きな色の部屋から順番に人を入れていくと、₆C₂×₄C₂ = 90 (通り)です

step2

ここからが本題です
step1で求めた90通りは各部屋に区別をつけた時の総数なので、step2で区別をなくして考える必要があります

やり方がよく分からない時に大切なのは、とりあえず書き出してみて考える、です
試しに、90通りのうち、「AとB、CとD、EとFがそれぞれ同じ部屋に入っている」ケースを書き出してみましょう

「AとB、CとD、EとFがそれぞれ同じ部屋に入っている」ケースは上図のように、
赤・青・緑の部屋の並び替えの総数、つまり6通り存在します

たしかに「AとB、CとD、EとFがそれぞれ同じ部屋に入っている場合」は、赤青緑の部屋を並び替えて(6通り)、その1パターンごとに、AとB、CとD、EとFを左から順に入れていけば、「AとB、CとD、EとFがそれぞれ同じ部屋に入っている場合」を全て考えているね！

お気づきでしょうか？
部屋の区別をなくすと、6つのいずれとも、全く同じになりましたよね！
このように部屋の区別をなくすと、区別があった場合の6通りがたった1通りにまとめられるんです！
上図では「AとB、CとD、EとFがそれぞれ同じ部屋に入っている場合」で考えましたが、他のケース、例えば「AとC、EとD、BとFがそれぞれ同じ部屋に入っている場合」などでも部屋に区別がある場合は6通り存在し、区別をなくすとたった1通りになります
つまりstep2で区別を無くすことで、90通りの内のあらゆる6通りが1通りにまとめられていくんですね！
最終的な答えは90通りを3!=6 (通り)で割ってあげて、90/3! = 15 (通り)です

90人の中から、6人につき１つグループをつくっていくとき、合計グループ数は90/6 = 15 (グループ)となるのと似ているね！

問題(4)の解き方

(4)は1人しか入れない2部屋どうしは見た目が同じで区別はできませんが、4人が入る1部屋は区別出来ます

step1

(3)と同様に、全ての部屋の区別がつくようにする必要があるので、1人しか入れない２つの部屋に赤・青色をつけて区別出来るようにしてあげましょう

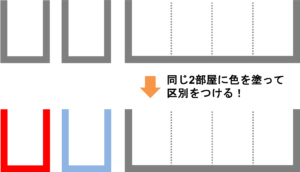
これで3部屋とも区別がついたので好きな色の部屋から順番に人を入れていくと、₆C₁×₅C₁ = 30 (通り)となります

計算を楽にするために、人数の少ない色の部屋から順番に選んだよ♪

step2

(3)と同様に、step2でつけた部屋の区別をなくしてあげる必要があります

試しに30通りのうち、「AとBがそれぞれ1人で部屋に入り、C,D,E,Fが同じ部屋に入っている場合」を書き出してみます

上図のように、赤・青の部屋の並び替えの総数、つまり2通り存在すると分かります
では次に部屋の区別を無くす、つまり元どおりの色に戻してみましょう

部屋の区別をなくすと、どちらも全く同じになりましたよね！
このように2部屋の区別をなくすと、区別があった場合の2通りが1通りだけにまとめられるんです！

したがって30通りの内のあらゆる2通りが1通りにまとめられていくので、最終的な答えは30通りを2!=2 (通り)で割ってあげて、30/2! = 15 (通り)となります

必ず解ける２ステップ

先ほど(3)ではstep1の値を3!で割り、(4)では2!で割りました
実はこの3や2は同じ人数の部屋数がいくつかあるかに対応していたんです

(3)は2人部屋が３つあり、(4)では1人部屋が２つあったよね♪

そのため、step2を少し書き換えると、組み分け問題を必ず解ける2ステップは以下のようになります！

これさえ覚えておけば、組み分け問題は絶対に解けるので必ず覚えておきましょう！

まとめ

いかがでしたか？
イラストを使うことで今までより本質的に組み分け問題が理解できたのではないでしょうか？
ぜひ2ステップをマスターして組み分け問題を得意分野にしてください！