問題集「黄チャート数1A」の質問とその回答をページ別にまとめています
同じ問題集をお使いのかたはぜひ復習にお使いください
目次
p182「正弦定理の利用」
(2)でA:B:C=1:2:9とA+B+C=180°から\(C=\frac{9}{1+2+9}\times{180}\)°となる理由が分かりません
回答
比の性質を知る必要があります
A:B:C=1:2:9のとき、(A+B+C):C=(1+2+9):9=12:9です
そして今A+B+C=180°です
これらの関係を表にすると以下のようになります
| 比 | 実際の角度 | |
| A+B+C | 12 | 180° |
| C | 9 | ? |
よって?に入るCの実際の角度は\(\rm{C}=\frac{9}{12}\times{180}\)°で求めることができます
例えばりんご6個をA君とB君でちょうど1:2になるようにわけるとき、A君がもらうりんごの数aは\(a=\frac{1}{1+2}\times{6}=2\)と求めることができるのと全く同じですね!
p192「三角形の内角の二等分線の長さ(1)」
p192の問題(1)で以下の2式
\[BD = \frac{sin\theta}{sin\alpha}AB \label{125-1} \\\]
\[DC = \frac{sin\theta}{sin\alpha}AC \label{125-2} \\\]
から
\[BD:DC = AB:AC \label{125-3}\]
が導かれる理由がなんとなくでしかわかりません
回答
比と分数を変換する必要があります
以下の関係式を覚えておきましょう!
ちなみに\(\Longleftrightarrow\)は同値(言い換え可能)であることを表しています
これは\(\frac{9}{12} = \frac{3}{4}\)は、9:12=3:4ともかけることからもわかると思います!
また\(\frac{a}{b}=\frac{c}{d}\)のとき、a : c = b : d も成り立ちますが、これは分数の性質を用いて以下のように言い換えていけば証明できます
\begin{align}
\frac{a}{b}=\frac{c}{d}&\Longleftrightarrow a\times{d} = b\times{c} \\
&\Longleftrightarrow a\times{d} = c\times{b} \\
&\Longleftrightarrow \frac{a}{c}=\frac{b}{d} \\
&\Longleftrightarrow a : c = b : d
\end{align}
今回は\(BD = \frac{sin\theta}{sin\alpha}AB \)を\(DC = \frac{sin\theta}{sin\alpha}AC \)で割ると
\begin{align}
\frac{BD}{DC}&=\frac{\frac{sin\theta}{sin\alpha}AB}{\frac{sin\theta}{sin\alpha}AC} \\ \nonumber
\Longleftrightarrow \frac{BD}{DC}&=\frac{AB}{AC}
\end{align}
となるのでBD : DC = AB : ACを導くことが出来ます
p200「三角形の内角の二等分線の長さ(2)」
別解のやり方と同じようにBDまで求めました
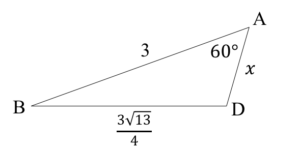
そして\(x\)の値をもとめるため三角形ABDにおいて余弦定理を利用すると
\[(\frac{3\sqrt{13}}{4})^2=3^2+x^2-2\cdot3{\cdot}x{\cdot}cos60^\circ\]
\[ x = \frac{3}{4}, \frac{9}{4} \]
と答えが2つ出てきたのですが、なぜでしょうか?
回答
2つの答えは以下の2パターンの図に対応しています
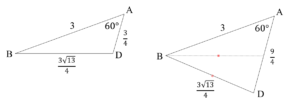
ADを求めるのに\(BD^2=\cdots\)として余弦定理を立てると2パターンの図が考えられるのでこのように答えが2つ出てくるんですね
なので余弦定理の式で答えが2つ出てきたときは図を書いてみて自分が考えているのが、どちらの図なのか考えてあげる必要があります
今回でいうと左図に対応するので答えは\(\frac{3}{4}\)ですね
答えではこのように2パターンの答えが出るのを避けるため、三角形ABCにおける余弦定理でcosBの値を求めてから\(AD^2=\cdots\)として余弦定理を用いています
p289「組み合わせと確率」
袋の中の白球と赤球を全て区別するとありますが、なぜ区別するのでしょうか?
白玉どうしと赤玉どうしは区別できないのではないですか?
また\({}_{n+5}{\rm{C}}_2=\frac{(n+5)(n+4)}{2}\)となる理由が分からないです
回答
PやCを使う場合は、必ず区別する必要があるためです!
例えば\({}_8{\rm{C}}_2\)は「区別のある異なる」8個から2個選ぶときの場合の数を表しています
「Cを使うためだけに勝手に区別して良いのか!?」と疑問に思うかもしれません
ただ確率では分母も分子もちゃんと区別して考えた場合の数を代入するなら、区別しないときと答えは一緒になるんです!
よくあるミスですが、分母だけ区別して分子だけ区別しないなどはNGです
分母を区別して考えているなら分子も区別し、分母を区別しないなら分子も区別しません!
次に\({}_n{\rm{C}}_m\)の計算についてですが、\({}_n{\rm{C}}_m\)は以下の定義で覚えておきましょう
\[{}_n{\rm{C}}_m =\frac{{}_n{\rm{P}}_m}{m!}\]
例えば\({}_8{\rm{C}}_2\)を求めるときは\(n=8,m=2\)として、
\begin{align}
{}_8{\rm{C}}_2 &=\frac{{}_8{\rm{P}}_2}{2!}\\
&=\frac{8\times7}{2\times1}\\
&=28
\end{align}
となります
よって\({}_{n+5}{\rm{C}}_2\)も同様にして、
\begin{align}
{}_{n+5}{\rm{C}}_2 &=\frac{{}_{n+5}{\rm{P}}_2}{2!}\\
&=\frac{(n+5)(n+4)}{2\times1}\\
&=\frac{(n+5)(n+4)}{2}
\end{align}
となります
p290「確率の加法定理(順列)」
解説途中に「2本のくじを取り出して、a,bの前に並べるときの場合の数」とありますが、並べるとは問題文に一言も書いてないのになぜ並べるんですか?
他の問題でも「並べる」と問題文で言われていないのに、並べようと思うことが出来ないです
回答
条件を満たす場合を書き出していった時に、並べているのと同じであると気づく必要があります
確率や場合の数では「分からないからとりあえず書き出そう!」と思うことが非常に大切です
今回の例でいうと、仮に当たりが4つだとして、それぞれA〜Dに対応させ、aとbが順にくじを引いて両方当たる場合を書きだして行くと、以下の図のようにA〜Dの4人から2人を選び並べている場合と同じになります
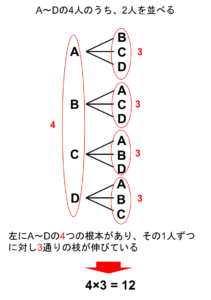
このように、まずは書きだしてみて、「これは並べている場合と同じだ!」と気づけるように演習を積みましょう!
p305「平面上の点の移動と反復試行」
Chart&Solutionに書かれている「これは、どの最短の道順も同様に確からしい場合の確率で」とはどういう意味ですか?
その下の解説は分かったのですが、上の式がダメな理由は分からないです
回答
「どの最短の道順も同様に確からしい」とは「最短となる全ての道順において、それぞれの確率が全て等しい」という意味です
もっと分かりやすい具体例で説明しましょう
以下のサイ君が出すサイコロ問題を考えてみてください
これは簡単ですよね!
出る目は全部で6通り存在し、1が出るのはそのうちの1通りなので1/6です
では同じサイコロを振って、2が出る確率はいくつでしょうか?
これも考え方は全く同じなので1/6です
同様に3が出る確率、4が出る確率、5が出る確率、6が出る確率も全て1/6となります
つまりどの目が出る確率も全て等しく1/6なんです!
このようにどの目の出やすさも等しい場合、どの目の出方も同様に確からしいと表現します
では「同様に確からしくない」のはどういうときでしょうか?
それはサイコロに一部細工が施されていて1の目だけ非常に出やすいなど、サイコロの各目の出る確率が異なる(各目の出やすさが異なる)場合を指します
今回の問題でいうと、地点Aから出発した人がPを通りBに到着する確率を「A→P→Bの経路の総数/A→Bの経路の総数」とするためには、分母の「A→Bの経路の総数」のいずれもが同様に確からしい(起こりやすさが全て同じ)必要があります
しかしChart&Solutionの後半に書かれているように、今回は道順によって確率が変わるため、同様に確からしくありません
そのため、場合分けして考える必要があります
一般的に「Aである確率」と言われて「Aである場合の数/全ての場合の数」と定義できるのは、分母の「全ての場合の数」のいずれもが同様に確からしい(起こりやすさが全て同じ)時のみであることを覚えておくようにしましょう
p353「円周角の定理の逆」
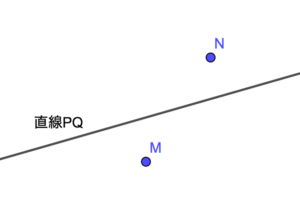
解答の最後の行の点線で「2点M,Nは直線PQに関して同じ側にある」と書いてあるのですが、これはどういう意味ですか?
回答
数学的な用語の1つですね
「2点M,Nは直線PQに関して同じ側にある」とは以下のような状態を指します
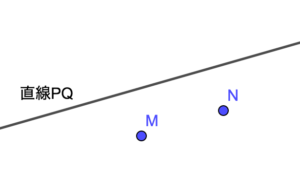
一方で「2点M,Nは直線PQに関して逆側にある」とは以下のような状態を指します